Le projet de recherche REPSAF porté par Hamid Chaachoua (LIG & INSPE, UGA) a été sélectionné pour obtenir un financement du pôle Pégase. Emmanuel Sander (IDEA, Genève), Jérôme Clerc (LPNC, UGA), Danielly Kaspary (LIG, UGA), Calliste Scheibling-Sève (LIG, UGA), Fabrice Guigon (professeur des écoles) et Yasmina Chaachoua (professeure des écoles) sont les autres membres du projet.
Au vu des résultats des évaluations nationales et internationales, la compréhension des fractions se heurte à d’importantes difficultés découlant de conceptions intuitives. En interrogeant le curriculum français du cycle 3, nous constatons que la résolution de problèmes reste marginale dans l’étude des fractions alors qu’elle est incitée pour les autres activités mathématiques. Pour favoriser le dépassement des limites induites par les conceptions intuitives des fractions, nous faisons l’hypothèse que la résolution de problème peut être un levier. Nous avons l’objectif de renouveler les progressions usuelles en élaborant une ressource pour le cycle 3, composée d’un corpus de problèmes et d’une progression qui favorise le développement d’une conception adéquate des fractions. Cette ressource, construite en mêlant les perspectives complémentaires de la didactique des mathématiques et de la psychologie du développement cognitif, sera testée au travers d’un essai randomisé contrôlé.
Situation générale et problématique
La résolution de problèmes doit être au coeur de l’activité mathématique des élèves tout au long de la scolarité obligatoire. Elle participe au questionnement sur le monde et de l’acquisition d’une culture scientifique, et par là contribue à la formation des citoyens. Elle est une finalité de l’enseignement des mathématiques à l’école élémentaire, mais aussi le vecteur principal d’acquisition des connaissances et des compétences visées. (Eduscol, 2018)
Ce premier paragraphe figure dans un bulletin officiel et résume un discours présent dans de nombreux autres documents ministériels. Il ancre la résolution de problèmes comme une approche d’enseignement propice au développement des compétences mathématiques, mais aussi au développement de ce que l’on peut appeler la culture mathématique – l’aptitude d’un individu à se servir des outils mathématiques pour mieux comprendre et agir face à une gamme de situations. Ce discours est également partagé par différentes approches scientifiques qui s’intéressent à l’enseignement et à l’apprentissage de cette discipline.
A cet égard, nous avons pu observer des changements de programmes scolaires conséquents au cours des trois dernières décennies aux cycles 1 et 2. Les élèves sont depuis le début de la scolarité invités à résoudre des problèmes impliquant les nombres entiers, même sans nécessairement disposer d’un large éventail d’outils mathématiques. Dans ce sens, les procédures personnelles des élèves sont valorisées et participent à la construction des modèles mathématiques. Nous constatons cependant une discontinuité de cette approche lors de l’introduction des fractions au cycle 3. La présentation de ces nouveaux nombres et l’outillage de techniques sont réalisés en amont de la résolution de problème, qui a conservé une participation seulement marginale dans l’enseignement de ces nombres. En revanche, les élèves sont paradoxalement souvent évalués par les situations problèmes convoquant les fractions. Or, le transfert des outils enseignés aux situations problèmes ne se fait pas tout seul, il s’agit bien d’une affaire de l’enseignement.
Lorsqu’on regarde la dernière évaluation nationale de début de sixième (2021), l’on retrouve la question suivante : « Une voiture roule à vitesse constante. Elle parcourt 80 km en une heure. Quelle distance parcourt-elle en un quart d’heure ? ». En considérant que « un quart d’heure » convoque un contexte familier pour la fraction, le calcul en jeu ne devrait pas poser problème. Or, nous sommes interpelés par le fait que seulement un peu plus de la moitié des élèves ont su répondre à cette question (taux de réussite de 54,8%). Selon les résultats de TIMSS 2019, le domaine « Nombre » pose particulièrement problème en France, son score est en retrait significatif par rapport au score moyen des pays européens. Sur cette évaluation, auprès des élèves de CM1, nous retrouvons deux autres problèmes impliquant les fractions et à chaque fois les taux de réussite de la France se sont avérés inférieurs aux taux de réussite en Europe et au niveau International (par exemple : taux de réussite de 13% en France, 29% en Europe et 28% au niveau International).
La conception d’une ressource qui pourra fournir aux enseignants du cycle 3 une aide à une véritable intégration des situations problèmes dans l’enseignement des fractions nous paraît donc impérieuse dans le contexte actuel.
Argumentation scientifique du projet
Au vu des résultats des évaluations nationales et internationales, il s’avère que la compréhension des fractions par les élèves semble se heurter à d’importantes difficultés, un fait signalé par les recherches en didactique depuis longtemps (Perrin-Glorian, 1985). Dans un premier moment, notre approche consiste à interroger le curriculum offert par une double entrée : didactique et psychologique. Cela nous permettra d’identifier ce qui existe et ce qui n’existe pas en matière d’enseignement sur les fractions, dans l’optique de d’élaboration d’une ressource qui a pour ambition de changer le scénario usuel.
À partir de l’entrée didactique, le savoir mathématique et les conditions et contraintes de sa diffusion sont objets de réflexion (Chevallard, 2010). La modélisation des types de tâches à partir de la notion de variables didactiques (Chaachoua et Bessot, 2019), permettra notamment d’identifier a priori les relations entre les techniques mathématiques et les situations problèmes, aussi bien d’un point de vue épistémologique qu’institutionnel.
À partir de l’entrée de la psychologie, l’identification des conceptions intuitives qu’ont les élèves de la fraction et qui s’avèrent limitantes afin de comprendre la notion est au coeur de notre étude. Que l’on parle de préconceptions (Ausubel 1968), de misconceptions (Clement 1982), de théories naïves (Carey 1985), de connaissances naïves (Fischbein, 1989), de raisonnements naïfs (Reiner et al. 2000), ou encore de savoirs en miettes (diSessa et al. 2004), il y a de commun qu’une certaine notion est conceptualisée à partir de connaissances préalables. Cela résulte en une conception restrictive par rapport à la notion concernée (Lautrey et al. 2008). Ainsi, les conceptions intuitives ont un champ de validité qui justifie leur existence et leur persistance, mais elles s’avèrent limitantes, il est alors crucial de les identifier pour mettre ensuite en place un travail de conceptualisation.
Pour renouveler l’existant sur l’enseignement de fractions, nous proposons de nous centrer sur une conception intuitive qui nous apparaît être au cœur des difficultés des élèves : la fraction comprise comme une structure bipartite (DeWolf et al., 2014 ; Lortie-Forgues, Tian & Siegler, 2015). Cette conception selon laquelle la fraction est composée de 2 nombres (a/b, c’est a sur b) est renforcée par le choix didactique qui alignent la forme a/b sur des contextes qui convoquent le sens parties/tout (DeWolf, et al., 2014). Même si en France, une des situations fondamentales proposées pour l’introduction des fractions est celle des longueurs (ERMEL, 1999), les fractions sont le plus souvent utilisées avec des quantités discrètes plutôt que continues. Le numérateur et le dénominateur y sont de mêmes unités (carreaux de chocolat, parts de pizza, parts de tarte, etc.). Ainsi retrouve-t-on chez les étudiants une préférence pour représenter les fractions sous forme de diagramme discret que continu (Rapp et al., 2015). Dérivant de cette structure bipartite, la fraction est, comme indiqué ci-dessus, plutôt vue comme relation entre 2 nombres et non comme un nombre, une magnitude : 2/8 c’est « deux sur huit » plutôt que « deux huitième » (Bonato et al., 2007). De la conception intuitive de fraction comme structure bipartite découle, par exemple, des stratégies erronées dans le cas d’addition de fraction. Ainsi, dans un énoncé comme celui de TIMMS (M041299, 2011) – Tom a mangé ½ d’un gâteau. Et Jeanne a mangé ¼ d’un gâteau. A eux deux, quelle fraction du gâteau ont-ils mangé ? – la stratégie intuitive est d’additionner séparément les numérateurs et les dénominateurs (soit 2/6). Or, en CM1, les élèves ne connaissent pas encore les techniques opératoires pour additionner les fractions qui peuvent être appliquées de façon algorithmique. La bonne réponse au problème traduit donc la capacité de l’élève à visualiser la fraction comme quantité : la moitié + le quart donne les trois quarts. Or on constate que le taux de réussite est faible y compris au niveau international (23%). Un enjeu majeur de l’enseignement des fractions est donc de favoriser la compréhension par les élèves d’une fraction comme magnitude.
Afin de favoriser le dépassement de la conception intuitive de la fraction comme structure bipartite, nous faisons l’hypothèse que la résolution de problème peut être un levier. Dans ce projet, il s’agit en particulier d’introduire des problèmes pouvant se résoudre selon deux stratégies distinctes grâce à l’adoption de l’un ou l’autre de deux points de vue – structure bipartite et magnitude (Scheibling-Sève et al., 2021). Les élèves doivent ainsi adopter les deux stratégies, favorisant le passage d’une conception à l’autre. En effet, c’est en articulant différents points de vue sur une même situation que l’élève peut embrasser sa complexité, Il s’agit de permettre à l’élève de catégoriser la situation : adopter un codage abstrait détaché des traits saillants et non profonds de la situation (Hofstadter & Sander, 2013). Durant les séances d’apprentissage, les élèves doivent catégoriser la situation via l’explicitation d’un changement de point de vue (Scheibling-Sève et al., 2021). Les élèves sont ainsi amenés à adopter plusieurs points de vue sur une même situation. Par exemple, un problème pour favoriser l’adoption des deux points de vue peut être le suivant : « Au goûter, il y a 2 cakes, un avec des noix et un avec des raisins. Julia, Yliès et Mylan veulent se partager les cakes. Ils veulent tous les 3 manger la même quantité. Quelle fraction de cake va manger Julia ? » Il existe 2 réponses possibles : Julia mangera 1/3 de chaque cake ou Julia mangera 2/3 d’un cake. Dans la conception bipartite de la fraction, la réponse de l’élève sera 1/3 de chaque cake, car cette conception consiste à partager chaque tout (ici un cake) en parties. Un énoncé alternatif introduira la phrase « Julia est allergique aux noix », susceptible de favoriser le deuxième point de vue. En effet, l’allergie de Julia au cake aux noix peut favoriser la solution de donner les deux tiers d’un cake aux raisins à Julia (Scheibling-Sève, 2019 ; Scheibling-Sève, Gvozdic, Pasquinelli & Sander, sous-presse). De plus, changer de point de vue sur un problème relève de la flexibilité cognitive, fonction qui soutient les apprentissages et leurs transferts à des situations nouvelles (Clerc & Josseron, 2021). Confronter des élèves à des changements de point de vue réguliers pourrait donc les amener à améliorer leurs capacités de flexibilité cognitive, ce qui sera testé ici en proposant des épreuves de flexibilité cognitive en pré-test et en post-test à l’ensemble des participants.
Afin d’évaluer la conception des fractions, il est utile de proposer des situations où la conception intuitive ne coïncide pas avec la conception experte. Nous parlerons par la suite de situations discordantes (Vamvakoussi, Van Dooren, & Verschaffel, 2012). Il s’agit de situations incompatibles avec la conception intuitive (Shtulman & Valcarcel, 2012). Dans ce cas, la réussite à cette situation discordante avec la conception intuitive peut être interprétée comme un indicateur de conceptualisation satisfaisante. Par exemple, pour évaluer si un élève adopte la connaissance experte de fraction comme magnitude et non comme structure bipartite, il est utile de comparer une paire de fractions discordante avec la conception intuitive de structure bipartite (2/9 et 1/3) en contraste d’une paire concordante avec la conception intuitive (6/8 et 7/9). Pour comparer correctement la paire de fractions discordante, la stratégie de comparer les numérateurs ou les dénominateurs ne peut fonctionner, il faut comparer la magnitude de chaque fraction. De même, le problème TIMMS (M041299, 2011) – Tom a mangé ½ d’un gâteau. Et Jeanne a mangé ¼ d’un gâteau. A eux deux, quelle fraction du gâteau ont-ils mangé ? – est discordant avec la conception intuitive. De précédents travaux (Scheibling-Sève, 2019 ; Scheibling-Sève et al., sous-presse) ont déjà mis en avant l’apport d’une progression fondée sur le dépassement des conceptions intuitives et favorisant les changements de points de vue. Cette progression, axée sur la proportionnalité, avait déjà favorisé l’adoption par les élèves d’une conception de la fraction qui n’est pas limitée à une structure bipartite. Au problème TIMMS M041299 (2011), les élèves de CM1 du groupe expérimental obtenaient un taux de réussite de 24% vs 13% pour les élèves du groupe contrôle et les élèves de CM2 du groupe expérimental obtenaient un taux de réussite de 41% vs 23% pour le groupe contrôle. En construisant une progression portant uniquement sur les fractions, on peut ainsi prédire des taux de réussite encore plus importants, témoignant d’une compréhension plus fine des fractions.
Objectifs et hypothèses
Notre objectif est de mettre en place, au travers de situations de résolution de problème, une progression soutenant le développement de la conception d’une fraction comme magnitude et non comme structure bipartite. Il s’agira d’identifier les meilleurs contextes favorisant le passage d’une conception de type bipartite à une conception de type magnitude. Outre l’élaboration d’une progression favorisant une conception de type de magnitude, des énoncés d’évaluation des conceptions seront conçus, fondés sur des situations discordantes avec la conception intuitive (Vamvakoussi, Van Dooren, & Verschaffel, 2012), c’est-à-dire pour lesquelles la conception bipartite est inadaptée pour trouver la solution alors que la conception de type magnitude le permet.
Nous souhaitons constituer une étude pilote permettant de s’assurer de la faisabilité et du caractère probant de la progression, à partir de ressources ayant certaines caractéristiques, destinée à soutenir l’apprentissage des fractions, qu’il est projeté de développer dans le cadre de l’action 4 du projet Pégase. Ainsi, si les résultats de l’expérimentation attestent leur efficacité, la cohorte « mathématiques » du cycle 3 de l’action 4 pourra s’emparer des productions de cette recherche (Ressources avec une progression).
Nous formulons deux hypothèses pour cette recherche :
Hypothèse 1 : La résolution de problème peut être mise à profit pour favoriser le développement d’une conception adéquate de la notion de fraction.
Hypothèse 2 : Il existe une progression de situations problèmes qui favorise la construction d’une conception de la fraction comme magnitude et le dépassement des limites induites par une conception d’une fraction comme structure bipartite.
Description du projet (méthode, planification)
Nous nous inscrivons dans une démarche de recherche collaborative entre chercheurs et enseignants (Bednarz, 2013). Ainsi, nous constituons une équipe de 4 chercheurs et 3 enseignants du cycle 3, du primaire et du collège, pour la co-élaboration de ressources qui s’appuiera sur des données issues de la recherche en psychologie du développement cognitif et en didactique des mathématiques. Deux chercheurs de l’équipe sont issus de la didactique des mathématiques (Chaachoua et Kaspary), deux chercheurs sont issus de la psychologie du développement cognitif (Sander et le post doc à recruter). Le choix des enseignants de l’équipe est fait par rapport aux critères suivants : formation des enseignants (Esteoule) ; enseignement CM1- CM2 (Esteoule et Mouffak) ; enseignement 6° pour intégrer la transition primaire collège (Bourgeois). Comme les ressources produites sont destinées à alimenter les ressources de l’action 4, nous avons veillé à intégrer les attentes de la cohorte cycle 3 et à créer les conditions de diffusion et d’appropriation des ressources produites par les acteurs de l’action 4.Cela sera donc assuré par Chaachoua, en tant que responsable de la cohorte cycle 3, et par Bourgeois et Kaspary membres du groupe de l’IREM responsable des ressources qui seront expérimentées dans le suivi longitudinal.
La première étape consiste à produire un modèle de référence qui caractérise les problèmes par rapport aux deux conceptions (bipartite ; magnitude).
La deuxième étape a pour objectif de produire les ressources. Pour cela, l’équipe conduira une analyse institutionnelle, qui s’appuie sur le modèle de référence, pour identifier ce qui existe, ce qui manque et ce qui peut exister dans l’enseignement des fractions en lien avec la résolution des problèmes. Les matériaux utilisés pour conduire cette analyse sont les programmes, les documents officiels et les manuels.
Trois résultats sont attendus :
– un corpus de problèmes, Rinst, usuellement présent dans les manuels.
– un corpus de problèmes, R, enrichi par la recherche et prenant en compte les conditions et contraintes institutionnelles, ainsi qu’une progression pour ces ressources, P.
– un plan de formation des enseignants pour les expérimentations. utilisés pour conduire cette analyse sont les programmes, les documents officiels et les manuels.
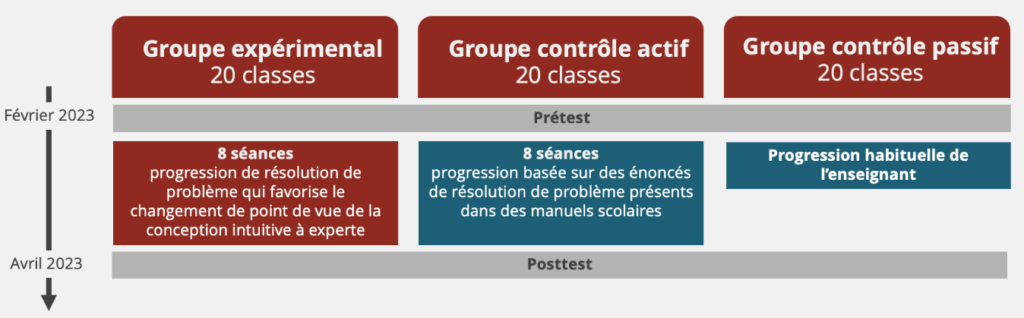
La troisième étape consiste à évaluer l’efficacité des ressources produites. Le protocole projeté est celui des essais randomisés contrôlés. 60 classes volontaires seront inscrites dans l’expérimentation. Les classes seront issues d’établissements REP et non REP. Un seul niveau scolaire sera ciblé, le CM1. C’est en effet en CM1 que les fractions sont introduites. Nous souhaitons en effet évaluer la progression auprès d’élèves n’ayant pas encore ancré leur conception intuitive. L’expérimentation aura lieu en amont de l’introduction des fractions par les enseignants. Les 60 classes seront réparties aléatoirement en 3 groupes :
– le groupe expérimental suivra la progression de résolution de problème qui favorise le changement de point de vue (de la conception intuitive de structure bipartite à la conception experte de magnitude) : (R, P).
– le groupe contrôle actif suivra une progression fondée sur des énoncés de résolution de problème de fraction usuellement présents dans des manuels scolaires, sans que les questions de congruence et d’incongruence soit explicitement introduits : Rinst.
– le groupe contrôle passif suivra la progression de l’enseignant.
L’expérimentation se tiendra au cours d’une période scolaire (du 20 février au 7 avril 2023). Sur la même semaine, les 3 groupes réaliseront, sur tablette, le même prétest dont les différents items seront issus des évaluations internationales TIMMS, du dispositif EvalAide, de précédents travaux de recherche ainsi de créations originales. Ensuite, durant une période de 4 semaines, chaque groupe composé de 20 classes travaillera sur sa progression respective à raison de 2 séances par semaine. Lors de la 6e semaine de l’expérimentation, les 3 groupes réaliseront le même posttest, identique au prétest.
En amont de l’expérimentation, les enseignants de chaque groupe recevront une formation de 2h par les expérimentateurs. Au cours de cette formation, les progressions, les principes d’apprentissage, les descriptifs des séances ainsi que le matériel nécessaire à leurs élèves leur seront présentés.
La quatrième étape sera centrée sur les analyses, rédaction d’articles, communication dans des congrès et diffusion vers le groupe de l’IREM, responsable de la production des ressources du suivi longitudinal.
Description des ressources à produire
Cette expérimentation aboutira à une progression d’apprentissage et des outils d’évaluation des fractions. La progression aura pour objectif le dépassement des limites induites par la conception intuitive de fraction comme structure bipartite et sera constituée de 8 séances de résolution de problèmes. Les outils d’évaluation seront constitués d’items discordants avec la conception intuitive de la fraction et adopteront les formes usuelles d’exercices utilisés par les enseignants (résolution de problème, comparaison de fraction…) afin qu’ils puissent les intégrer dans leurs propres évaluations. L’ensemble de ces ressources (Corpus de problèmes, Progression, Pré et post tests, Plan de formation) est pensé pour une diffusion à l’action 4 entre septembre et décembre 2023.





